| Setting up your Optimization problem |
| 1. Normalizing Inputs |
| 2. Vanishing & Exploding Gradients |
| 3. Weight Initialization for network |
| 4. Numerical approximation for gradients |
| 5. Gradient Checking |
1. Normalizing Inputs
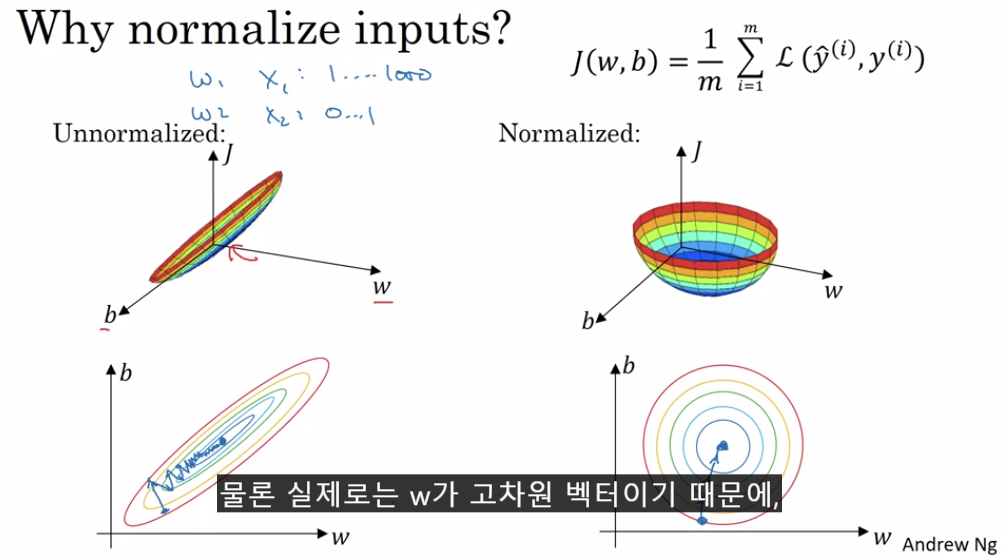
1) Normalization 을 하는 이유
Normalization을 하지 않아도 NN은 W와 b를 J를 최소화 하는 방향으로 update할 것이다. 다만, 위와 같이
Weight(b포함) 의 그래프가 Normalization했을 경우에 비하여 짜부되어 물리적으로 계산 효율이 떨어지는 것.
hleecaster.com/ml-normalization-concept/
정규화(Normalization) 쉽게 이해하기 - 아무튼 워라밸
데이터 정규화는 머신러닝에서 꼭 알아야 하는 개념이다. 매우 훌륭한 데이터를 가지고도 정규화를 놓치면 특정 feature가 다른 feature들을 완전히 지배할 수 있기 때문이다. 최소 최대 정규화, Z-
hleecaster.com
이거 참고
2) 주의점
- Train set의 평균과 표준편차를 이용하여 Train set을 표준화하는데(물론 표준화 방법은 여러 방법이 있겠지만 여기서는 이 방법을 예로 든듯), Test set에도 Train set에서 구한 평균과 표준편차를 그대로 이용하여 Normalization시킨다. 그 이유는 Test set의 정의에서 비롯되는데, 명심해야할 것은 Train set는 우리가 모델을 만들기 위해 학습시키는 데이터이고 Test set은 단지 성과 측정을 위함이다. 따라서 우리가 만든 모델을 Test set에 맞추는 행위는 바보같은 짓이다. 그렇게 하면 자연스레 성과가 좋아지겠지...
- Normalization의 포인트는 피쳐간의 범위를 동일화시켜주는 것이다.
만약 x1:0~1000, x2:0~1000 이라면 Normalization이 필요없을 것이다. ( 아닐 수도 있다 ㅋㅋ )
하지만 x:0~5, x2:0~1000 이라면 둘 다 Normalization을 하여 그 평균과 분산을 맞춰주는 것이 좋을 것이다.
사견으로, 이것저것 복잡하게 생각할 것 없이 Normalization하면 될듯.
2. Vanishing & exploding gradients

W가 1보다 크거나 작을 때, layer의 수가 크다면 마지막 산출값 (y hat)이 무지막지하게 크거나 작을 것이다. 이는 층을 지날 때마다 W가 계속해서 곱해져서 나타나는 현상인데, 이렇게 되면 L(Y, Y_hat)을 통해 W를 update하는 과정이 길어질 것이다. 왜냐하면 Y와 Y_hat 과의 간극이 커지기 때문이다. -
- activation 함수로 sigmoid를 사용할 경우, input data의 범위가 어떻든 간에 0~1으로 output을 산출하며 층이 깊어질 수록 좁은 범위로 수렴하게 된다(예를 들어 0.45~0.55). 이렇게 되면 초기 층의 W 값이 큰 폭으로 변화하여도 끝에 가면 큰 변화가 없어진다. 즉, dW[초기층] 이 0에 가까워져 초기 parameter W의 update가 매우 느려진다. Relu를 사용하는 이유 중 하나이다.
- (뇌피셜) Relu를 사용한다고 해결이 될까? Relu의 경우 산출범위가 0~무한대로 자유롭긴 하지만, 만약 층이 깊고 모든 층의 W가 0보다 작으면 마지막 output이 0으로 수렴하게 되어 위와 같은 문제가 또 발생한다. 반대로 모든 층의 W가 1보다 크다면 폭발적으로 gradient(dW)가 커진다. 왜냐하면 y_hat과 y의 격차가 어마무시하게 커질 것이기 때문.
전자는 gradient가 너무 작아 update가 느릴 것이고, 후자는 y_hat과 y의 격차가 너무 커 update가 오래 걸릴 것이다.
물론 계속해서 update하면 적절한 W와 b를 찾을 수 있겠지만, 계산 과정이 길어짐.
So, W를 잘 initialize 하여 이런 현상을 최소화 하여야 한다.
3. Weight initialization for network
1) 문제제기
앞서 살펴본 것처럼 W값에 따라서 Vanishing or exploding 하는 문제가 발생한다. 이를 최소화하기 위해서는 W를 적절하게 타협하여 조절하는 것이 중요함.
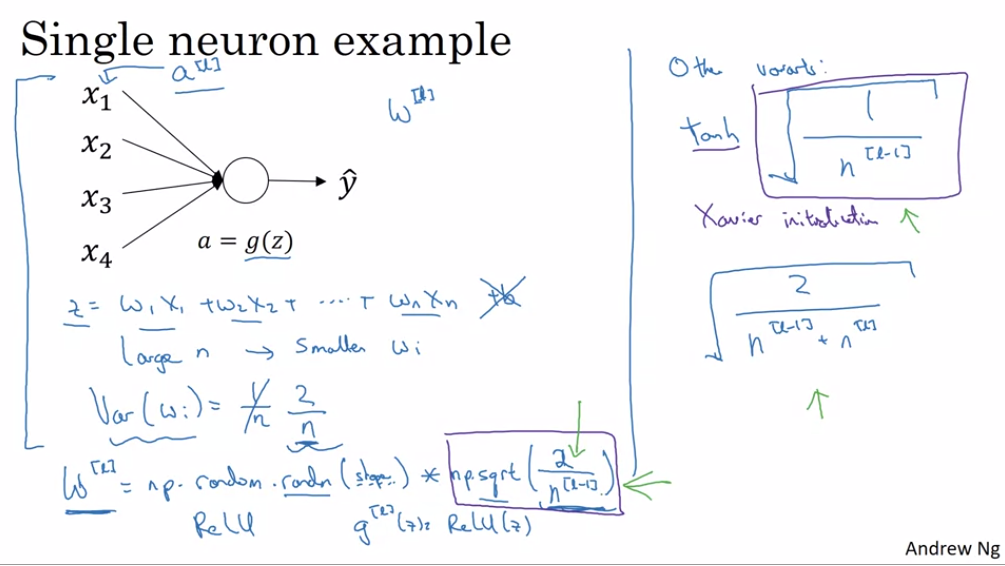
2) 기본 idea는 다음과 같다.
먼저, 위의 그림에서 확인할 수 있듯이 n이 커지면 커질 수록 다음 층의 Z 값이 커지므로( 아직 W에 대한 적절한 제한이 이루어지지 않은 상태이며 X는 고정이므로 일반적으로 얘기하는 것) Wi가 작아져야 한다(X는 입력값으로서 고정되어 있음).
Wi가 작아진다는 것은 Wi가 음수로 떨어지는 것이 아니라 0과 가까워진다는 의미. 즉, n에 따라서 Wi의 크기를 조절하여 Z값이 너무 작아지거나 커지는 것을 방지한다.
2) 방식은 다음과 같다.
1st. Wi의 크기를 n에 맞게 조절해야 하므로 Var(Wi)를 1/n 으로 만들어준다. (activation 함수가 Relu인 경우 2/n)
- 그 이유는 다음과 같다. 앞서 설명했듯이 Vanishing과 Exploding의 문제점은 산출값이 계속해서 커지거나 작아지는 것.
즉, 층을 지날 수록 산출값의 평균과 분산이 바뀌는 것이 문제이므로, 층을 지나도 산출값이 어느정도 유지 된다면 문제를 개선할 수 있다. 따라서, Var(Wi)를 위와 같이 설정한다면 node가 많을 때 Wi를 0에 가깝게 설정할 수 있고, node가 적을 때 Wi를 좀 더 0과 멀리 떨어진 범위까지 허용하게 되므로 n 의 크기에 따라 다음 층의 산출값을 조절할 수 있다.
=> " 자동 산출값 범위 조절 프로그램"이라고 이해하자.
2nd. 코딩은 그림과 같은데, 설명하자면 평균이 0이고 분산이 1인 matrix를 생성하고 이를 np.sqrt(1/n)으로 나누어 Var(Wi) = 1/n이 되도록 만든다.
a = np.random.randn(), var(a) = 1, mean(a) = 0 이므로 Wi = a*np.sqrt(1/n). var(Wi) = (1/n) * var(a) = 1/n.
mean(Wi) = 0
- 입력층이 평균 0 , 분산 1로 정규화되었다고 가정한다면 mean(X) = 0, var(X) =1이라고 할 수 있다.
이 때, mean(WX) = 0, var(WX) = 1 이므로 다음 층의 입력값(A[l])도 전 층의 입력값(A[l-1])과의 분포가 비슷해진다.
cf) 이 논리에는 전제가 있다. 먼저 activation 함수가 sigmoid라는 점, Wi의 분산을 1/n 으로 설정한 것 또한 sigmoid 함수의 선형적인 부분에 들어가게 하려는 설정인듯. 그렇게 해야 activation(sigmoid)함수를 적용해도 A[l]의 분포가 거의 변하지 않아 또한, var(WX) = 1은 완벽한 등식이 아니다. 수학적으로 공분산을 고려해야 하지만, initialization의 목적은 "어느 정도" 입력층의 분포를 비슷하게 하려는 목적이니 만족하자.)
3) Other Variance
- Var(Wi)를 1/n 으로 설정하는 것은 sigmoid 함수일 때 이다.
- activation 함수에 따라서 Var(Wi)를 적절하게 바꿔줄 필요가 있다. 왜냐하면 어떤 activation 함수인지에 따라 선형적인 부분이 다르기 때문이다.
- 연구에 따르면 relu는 np.sqrt(2/n),
tanh 는 np.sqrt(1/n) 혹은 np.sqrt(2/n[l-1]*n[l])로 사용하는 듯하다.
4) 결론
이처럼 Wi의 분산을 무엇으로 설정하는지가 hyper - parameter로서 하나의 매개변수가 된다.
하지만 교수님에 따르면 다른 중요한 hyper - parameter에 비해 엄청 중요한건 아니니 알아두자.
4. Numerical approximation of gradients

이건 그냥 그림보면 알 수 있음. 미분의 기본 정의와 관련되며 two-sided difference를 이용한다는 뭐 그런 얘기
5. Gradient Checking
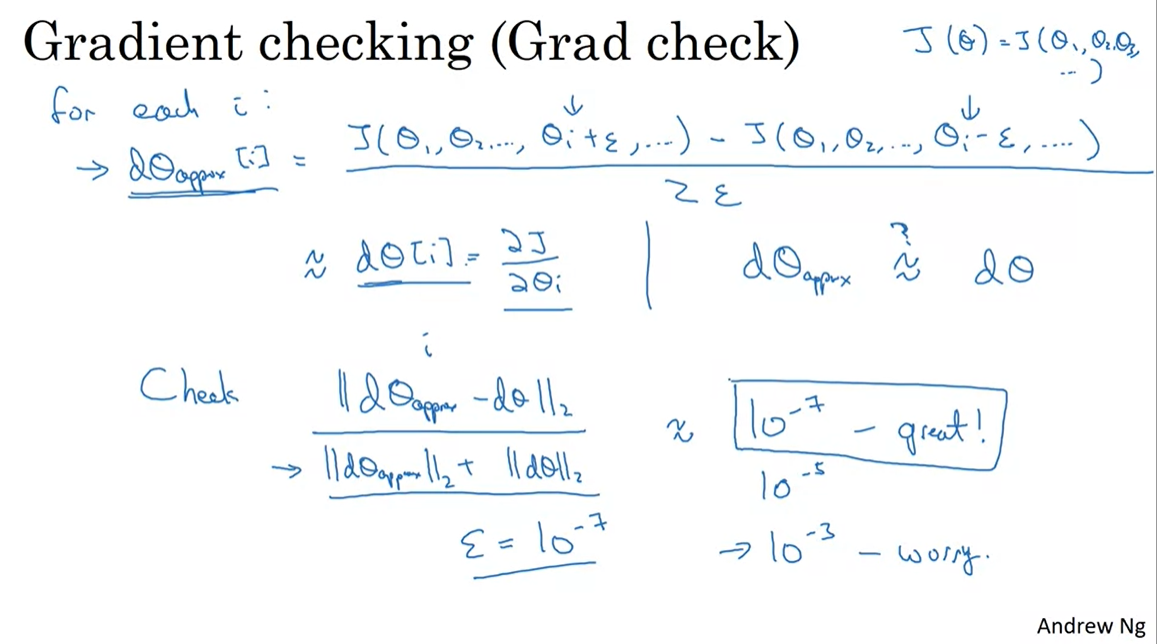
- 앞서 살펴본 two-sided difference를 이용한 기울기 근사값을 back propagation을 이용하여 구한 기울기와 비교하여 back propagation이 잘 이루어지는가 비교해볼 수 있다.
- 위와 같이 앱실론을 매우 작은 값으로 설정하고, 위의 공식을 적용하여 2가지 방식으로 구한 기울기를 비교함.
만약 10의 -7승을 앱실론 값으로 설정한다면 공식으로 구한 값이 10의 -7승 보다 작을 때 훌륭하게 back propagation을 수행하고 있다고 판단 가능.
- 분모로 나누어준 것은 값을 표준화하기 위함.
질문과 비판은 언제나 환영입니다. 많이 꾸짖어 주십쇼.
'DeepLearning Specialization(Andrew Ng) > Improving Deep Neural Networks' 카테고리의 다른 글
| [Week 3] 1. Hyperparameter tuning (0) | 2020.10.24 |
|---|---|
| [Week 2] Programming Assignments (0) | 2020.10.24 |
| [Week 2] 1. Optimization Algorithms (0) | 2020.10.23 |
| [Week 1] Programming Assignments (0) | 2020.10.23 |
| [Week 1] 2. Regularizing your neural network (0) | 2020.10.18 |

