728x90
1. 다항회귀 적용의 문제점


일반적인 선형회귀와 같다.
그런데 선형회귀의 전제는
- 서로 다른 시점의 잔차가 등분산성을 가져야 하고,
- 서로 다른 시점의 잔차가 독립(공분산 = 0) 이어야하는데, 시계열 데이터의 경우 시점 간에 독립성을 보장할 수 없으며 오히려 연관성이 짙다. 따라서 다른 접근법이 필요하다.
cf) 참고로 잔차의 독립성은 Durbin-Watson test로 검정한다.
<선형회귀의 잔차에 대한 글>
mindscale.kr/course/basic-stat-r/residuals
잔차분석
mindscale.kr
2. AutoCorrelation(자기상관성)
1) 개념

- 그 접근법이 autocorrelation이며 여기서 auto는 self의 의미이다.
- 이게 무슨의미냐면 변수 x를 shift한 변수를 하나 만들고 둘 사이의 공분산을 연산하는 것.
- 즉, 자기자신으로부터 나온 변수와의 비교이기 때문에 auto 이다.
- 이를 통해 x변수가 시점에 따라 그 자신과 correlation이 있는지 파악할 수 있는 것.
2) 종류
- autocorrelation 은 다음과 같이 positive, negative, random(None)의 경우로 나뉜다.
- Positive : 잔차가 같은 부호로 이어질 경우.
- Negative : 잔차의 부호가 계속 바뀜.
- Random : 자기상관성이 읎다.


3) How to check?

- 그래서 자기상관성이 있는지, 있다면 neg인지 pos인지 우째 판단할 것이냐~
- 위와 같이 시각화해서 알 수도 있지만, 이는 주관성이 개입되므로 수치로 증명할 필요가 있다.
- 참고로 여기서 residual 은 잔차, error term 은 오차를 의미한다.
- 오차(epsilon) : 모집단의 회귀식에서 예측된 값 - 실제 관측값
- 잔차(e) : 표본집단의 회귀식에서 예측된 값 - 실제 관측값
- 오차는 알 수가 없으니까 잔차를 사용한다.
[ Positive Autocorrelation 검정 ]

- 귀무가설은 p=0 즉, 자기상관성이 없다는 것.
- 대립가설은 p>0 즉, positive 자기상관성이 있는 것.
- 그 기준은 변수 x와 x'로부터 구한 회귀식과 잔차인 e로부터 구한 d 값으로 한다.
- d 는 수식상으로 positive correlation일 경우 시점i와 시점i-1에서 잔차의 부호가 같을 확률이 커서 e_i와 e_i-1의 차이가 적다. 따라서 특정 threshold dL 을 정하고 그 이하일 경우 귀무가설을 기각하고 대립가설을 채택한다.
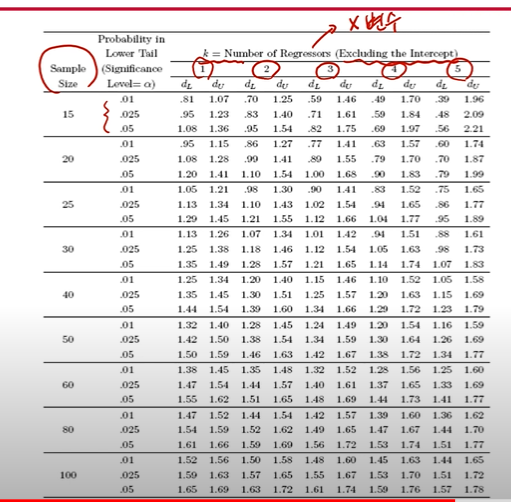
- 그리고 그 threshold dL과 dU는 위와 같이 정하면 됨.
- 단측검정이므로 dL보다 d가 작으면 귀무 기각하고 대립가설 채택함. 아마 dU 는 dL보다 조금 더 오른쪽에 있어서 그 사이값을 '애매하다'라고 규정하여 결정을 포기한듯. 아싸리 d가 dU보다 높은 경우만 확실하게 귀무가설을 채택한다고 이해하고 넘어감.
[ 예시 ]
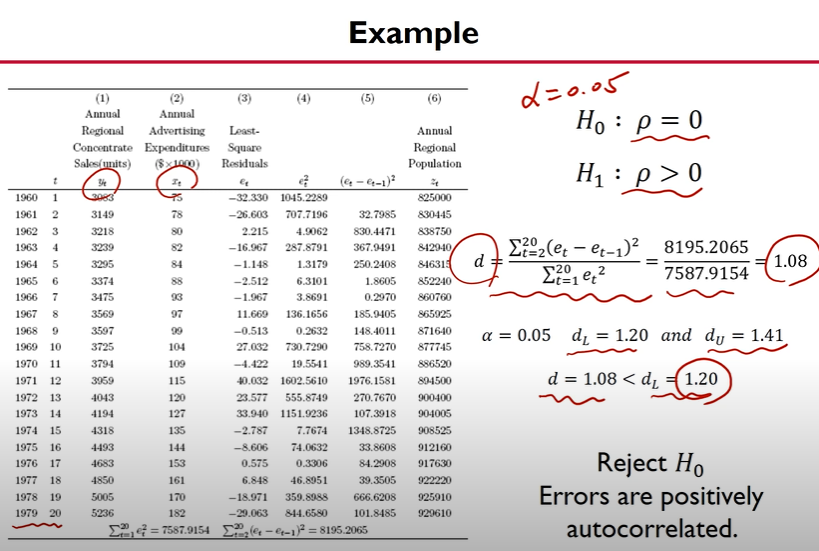
- 위 예시에서 xt는 t 그 자체는 아니지만 어느 정도 시간에 따라 선형적으로 늘어나는 변수이고, 이 변수의 auto-correlation을 조사하고자 한 것.
- 만약 auto = 0 이면 일반적인 회귀모델을 사용할 수 있지만, 그렇지 않다면 autocorrelation이 존재하므로 최소제곱법을 이용한 회귀분석이 불가능.
- 예시는 positive autocorrelation이므로 기존 회귀분석 적용 불가능.
[ Negative Autocorrelation 검정 ]

- negative autocorrelation의 경우, (4-d)를 dL 및 dU와 비교한다. d 값이 커질 수록 4-d 값이 작아지는 원리를 이용.
- 4라는 숫자를 이용한 이유는 d값의 분포가 4에서 빼주었을 때, 기존 유의수준과 dL, dU 값을 일률적으로 적용할 수 있어서가 아닐까 생각한다. 엄청 중요한건 아니니 대충 이렇게 이해하자.
[ 몇가지 참고사항 ]

- nth-order는 n만큼 shift한걸 변수로 활용한다는 의미. Durbin-Watson test 는 1st order 밖에 확인할 수 없지만 higher order는 어떻게 알 수 있는지 나중에 알려준다고 함.
- 주로 Positive인 경우가 많다.
3. Time Series with Seasonal Variations
1) Seasonal Variation
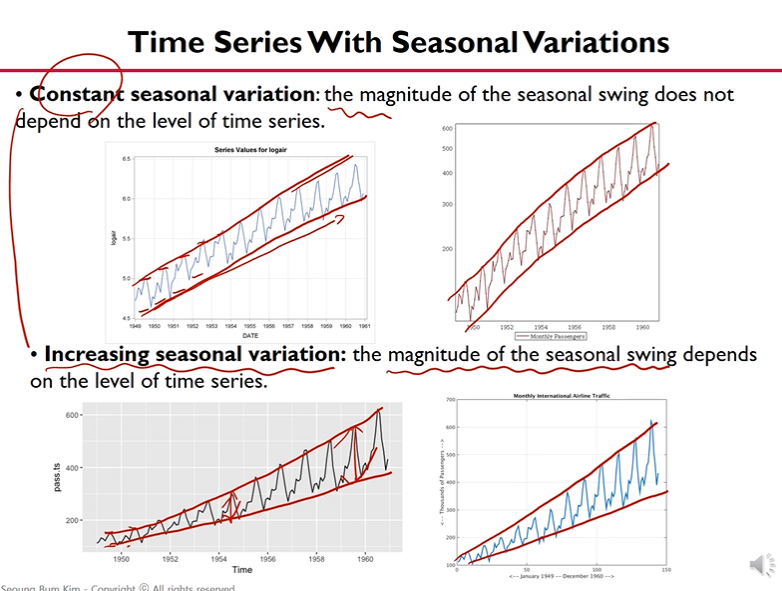
- 폭이 일정한지 여부에 따라 둘이 나뉨.
- Increasing seasonal variation의 경우 모델로 핸들링하기가 까다로움.
2) Increasing Seasonal Variations 핸들링

- 두가지 방법이 있다.
- 람다를 제곱해주는 것.
- 자연로그변환을 해주는 것. 이걸 더 자주 사용함.
728x90
'김성범 교수님 유튜브 강의 > 파이썬 시계열 분석' 카테고리의 다른 글
| ARIMA 모델 개요 - Part 3 (0) | 2021.01.12 |
|---|---|
| ARIMA 모델 개요 - Part 2 (0) | 2021.01.10 |
| ARIMA 모델 개요 - Part 1 (0) | 2021.01.10 |
| 시계열 분석 기초(Time Series Regression) - Part 3 (0) | 2021.01.09 |
| 시계열 분석 기초(Time Series Regression) - Part 1 (0) | 2021.01.07 |



