| Batch Normalization | |
| 1. Normalizing activations in a network | |
| 2. Fitting Batch Norm into a neural network | |
| 3. Why does Batch Norm work? | |
| 4. Batch Norm at test time |
1. Normalizing activations in a network
1) 기본개념

Normalization이 필요한 이유에 대해서는 Opimization 강의노트에 자세히 기술했으니 참고 바란다.
학습 속도를 높이기 위해 feature들을 Normalization하는 작업은 꼭 필요한데, 이를 통해 feature들의 scale을 맞춰주어 gradient descent 의 속도를 물리적으로 높일 수 있기 때문이다. 이건 deep neural network에도 똑같이 적용된다.
이전에 Logistic Regression에서는 입력층에서만 Normalization을 적용했으나, NN에서는 각 층의 모든 유닛들에 적용을 하는 것이다. z[l]을 Normalization하여 W[l+1], b[l+1] 을 빠르게 update하는 효과를 볼 수 있는 것.
참고로 z[l]과 a[l] 중 어느 것을 정규화해야하하는지에 대한 논란이 있지만 일반적으로 z를 정규화 한다. 그리고 당연한거지만, z[2]를 정규화 한다는 말은 z[2]에 포함되어 있는 각각의 유닛들을 정규화시킨다는 말이지 z[2](1), z[2](2), ... 등 각 유닛들 전체의 평균과 분산을 구하여 빼주고 나눠준다는 이상한 생각을 하면 안된다.
즉, z[l]의 첫번째 유닛은 그 첫번째 유닛에 들어가는 m(num. of training set)개의 data에 대해 평균과 분산을 구하여 그 값을 이용하여 정규화 된다.
2) Implementing

이걸보고 띠용할 수 있다. 감마랑 베타는 왜 튀어나오는가?
먼저, 정규화한 변수는 평균이 0, 분산이 1인 변수가 된다. ( 저 앱실론은 분산이 0이 되는 경우 계산이 꼬이므로 계산의 안정성을 위해 추가해놓은 것)
그런데 우리는 항상 평균이 0이고 분산이 1인 유닛을 원하는 것이 아니다. activation 함수가 sigmoid 인 경우, z값이 0주변에 밀집되면 함수는 선형적인 특성을 띈다(그림에서 확인할 수 있듯이 sigmoid 함수의 직선과 유사한 부분에 속하므로). 결과적으로 우리는 Neural Network의 장점인 비선형성을 잃게 되므로 모든 유닛이 선형적으로 된다면 비선형적인 함수를 산출할 수 없고 이는 변화무쌍한 데이터에 유연하게 대처할 수 없음을 의미한다.
따라서 정규화한 z_norm을 다시 감마와 베타를 이용해 rescale 하여 원하는 평균과 분산을 가진 유닛(z_tilde)로 만들어준다. 이렇게 되면 감마와 베타라는 새로운 변수가 나타나게 되는데 감마는 분산, 베타는 평균과 관련이 있다.
2. Fitting Batch Norm into a neural network
1) Adding Batch Norm
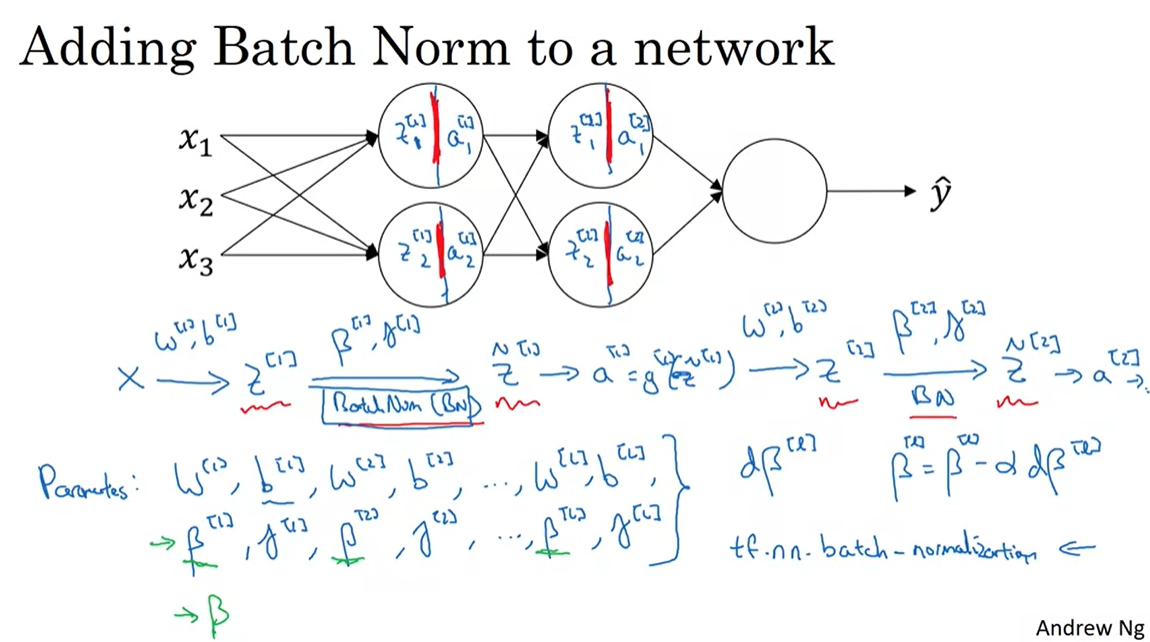
위와 같은 일련의 과정을 거치면서 z[1]을 정규화하고 그렇게 나온 z_tilde[1]을 이용해 z[2]를 구하고 이걸 또 정규화한다. 쭉쭉쭉
이해하기 쉽게 말하자면 원래는 유닛안에서 z를 생성하고 activation 함수를 이용해 a를 산출하는 2 단계가 이루어지나, 이제는 중간에 z를 z_tilde로 바꾸는 정규화 과정이 추가되었다고 생각하면 된다.
우리는 이제 W, b, beta, gamma 이 4가지를 update 해야한다. 그런데, 자세히 살펴보면 z를 z_norm으로 만드는 과정에서 평균을 빼주고 표준편차로 나누어주는데 이 과정에서 b 값은 사라진다. 따라서 우리는 이제 b를 고려할 필요가 없어지므로 z = wa 로 정의하고 시작하면 된다.
2) Working with mini-batches

mini batch를 적용시킬 때도 마찬가지이다. 그냥 하면 된다.
그런데 parameter의 dimension에 대한 설명을 보면 모든 변수는 (n[l],1) 형태를 갖는다고 하는데, 나는 이 부분이 왜인지 헷갈렸다. 왜 m이 아니라 1인가.... m개의 training set 을 통해 평균과 분산을 구하고 그것을 정규화에 이용한다는 생각이 머리에 박혀 저 말이 왜인지 헷갈렸다. 단순히 생각하면 되는데.
즉, 정규화 과정에서 m개의 training set이 필요한 것은 맞지만 그걸로 유닛별 평균과 분산을 구하면 끝이다. 이걸로 개개의 single example 을 넣어 베타와 감마값을 구해볼 수 있는 것이다. 물론 이를 vectorizing하면 (n[l],m) 형태의 matrix가 되겠지.

코드화하면 위와 같다.
1 mini-batch에 1 update 하는 것으로, 당연히 momentum, RMSprop, ADAM 모두 적용이 가능하며 단지 beta와 gamma가 추가된 것 뿐임.
3. Why does Batch Norm work?
1) Covariate Shift

데이터의 변화가 생길 경우, 그 변화에 의해 알고리즘을 수정해야할 상황이 있고, 그 데이터의 변화를 Covariate Shift라고 한다. 위의 예시에서 검은 고양이만 학습시켰다가 컬러풀한 고양이 데이터를 넣으면 제대로 작동못하는 상황이 생김.
2) NN에의 적용

NN에서 layer=3의 경우 layer2의 산출값을 입력값으로 받는데, 그 값들은 더 왼쪽의 W와 b 값들에 의해 매 update마다 다른 데이터가 된다. 따라서 앞서 언급했던 'Covariate Shift' 문제가 발생하여 빠르게 W[3]와 b[3]가 최적으로 수렴하는데 방해가 될 수 있다. 따라서 Batch Normalization을 통해 입력값의 변동폭을 줄여주면 어느 정도 문제를 완화시킬 수 있다. Batch Normalization을 적용해도 데이터가 변하는 것은 똑같으나 mean과 variance가 동일하므로 어느 정도 비슷한 범위에서 움직이는 것.
변동폭을 줄임으로써 전층과 다음층 간의 연결고리를 느슨하게 하여 각 층이 서로 좀 더 독립적으로 학습할 수 있게 한다고 하는데 이건 잘 이해안됨.
3) 갑자기 분위기 Regularization?
mini-batch로만 평균분산을 구하면 전체에 비해서 noise가 있기 때문에 z[l]로 z_tilde[l]을 구할 때 더 noisy하다. 유닛들에 noise를 더함으로써 특정 유닛에의 의존도를 낮춰주어 Regularization이 효과가 있다. 큰 효과는 아님. 물론 mini-batch size가 클 수록 그 noise가 작아질 것이기에 효과는 반감.
교수님은 이걸 Regularization의 수단으로 사용하는 것을 추천하지 않음.
4. Batch Norm at test time

이 부분은 바로 이해가 안되서 구글링을 좀 해봤다.
요약하자면, Train time에는 mini-batch별로 평균과 분산을 구해서 normalize했다면 test time에서는 train time에서 구해왔던 mini batch들의 평균과 분산을 exponential moving average( 전에 살펴봤던 이동평균기법 )을 이용해서 구한 평균과 분산으로 normalize 한 후 그걸로 test를 실행하는 것.
test를 하는거니까 당연히 test set으로 평균과 분산을 구해서는 안될 것이며, 모든 update를 마친 후 전체 train set을 통해 구한 유닛 별 평균과 분산을 이용하는 것이 아니라, training 과정에서 얻어진 평균과 분산을 이용하는 이유는 아마 계산 효율이 아닐까 조심스레 추측해봅니다.
요거 참고
딥러닝 용어정리, Batch Normalization, 배치 정규화 설명
제가 공부한 내용을 정리하는 글입니다. 작성의 편의를 위해 아래는 반말로 작성하였습니다. 잘못된 내용이 있다면 지적 부탁드립니다. 감사합니다. Batch Normalization 배치 정규화의 목적 Batch norma
light-tree.tistory.com
비판과 비난은 언제나 환영입니다. 많이 꾸짖어주세요.
'DeepLearning Specialization(Andrew Ng) > Improving Deep Neural Networks' 카테고리의 다른 글
| [Week 3] 4. Introduction to programming frameworks (0) | 2020.10.25 |
|---|---|
| [Week 3] 3. Multi-class classification (0) | 2020.10.25 |
| [Week 3] 1. Hyperparameter tuning (0) | 2020.10.24 |
| [Week 2] Programming Assignments (0) | 2020.10.24 |
| [Week 2] 1. Optimization Algorithms (0) | 2020.10.23 |


